Katika hisabati, muhtasari (unaoashiria kwa ishara kubwa ya Kigiriki sigma) ni seti ya muhtasari wa nambari. Kiasi gani? Haya ni matokeo ya kitendo kama hicho. Ikiwa nambari zitaongezwa moja baada ya nyingine kutoka kushoto kwenda kulia, basi matokeo ya kati ni jumla ya kiasi.
Kiasi gani?
Nambari zitakazofupishwa zinaweza kuwa kamili, za kimantiki, halisi au changamano. Kwa kuongezea, aina zingine za maadili zinaweza kuongezwa: vekta, matrices, polynomials, na kwa ujumla vipengele vya kikundi chochote cha kuongezea (au hata monoid).
Ikiwa idadi ya vipengele vya istilahi ni kikomo, basi majumuisho hutoa thamani iliyobainishwa vyema kila wakati. Muhtasari wa mlolongo usio na kipimo wa maadili huitwa mfululizo. Thamani yake mara nyingi inaweza kuamuliwa kwa kutumia kikomo (ingawa wakati mwingine thamani inaweza kuwa isiyo na kikomo).
Msururu
Muhtasari wa nambari [3, 7, 2, 1] unaweza kufafanuliwa kwa usemi ambao thamani yake ni jumla ya nambari zilizojumuishwa ndani yake, kwa mfano 3 + 7 + 2 + 1=13. nyongezakwa ushirika, jumla haitegemei jinsi maneno yamewekwa katika vikundi, kwa mfano, (3 + 7) + (2 + 1) na 3 + ((7 + 2) + 1) zote ni tisa, kwa hivyo mabano kawaida hutolewa.. Nyongeza pia ni ya kubadilisha, kwa hivyo kupanga upya masharti hakubadilishi thamani ya jumla. Kumbuka kuwa mali hii haiwezi kufanya kazi kwa muhtasari usio na kikomo.

Hakuna nukuu maalum ya mpangilio wa muhtasari wa aina hii. Kuna nuance kidogo tu ikiwa kuna chini ya vipengele viwili. Muhtasari wa mlolongo wa mshiriki mmoja hauna ishara ya kujumlisha (haiwezi kutofautishwa na umbo la nambari yenyewe), na ikiwa hakuna vipengele hata kidogo, basi haiwezi hata kuandikwa (lakini badala yake inaweza kuashiria na. thamani yake "0"). Ikiwa, hata hivyo, masharti ya mfuatano yamebainishwa na muundo maalum, kama vile chaguo za kukokotoa, basi opereta wa majumuisho anaweza kuwa muhimu au hata muhimu.
Rekodi
Ili kuelewa jumla ni nini, ni muhimu pia kuchanganua mwonekano wake.
Ili kujumlisha mlolongo wa nambari kamili kutoka 1 hadi 100, usemi mara nyingi hutumiwa unaojumuisha duaradufu ili kuonyesha washiriki waliokosekana: 1 + 2 + 3 + 4 + … + 99 + 100. Mchoro ni rahisi kuona katika mfano huu. Hata hivyo, kwa chaguo ngumu zaidi, ni muhimu kutaja hasa sheria inayotumiwa kupata thamani ya vipengele, ambayo inaweza kupatikana kwa kutumia "Σ" operator wa muhtasari. Kwa kutumia ishara hii (sigma), unaweza kutumia nukuu ifuatayo:
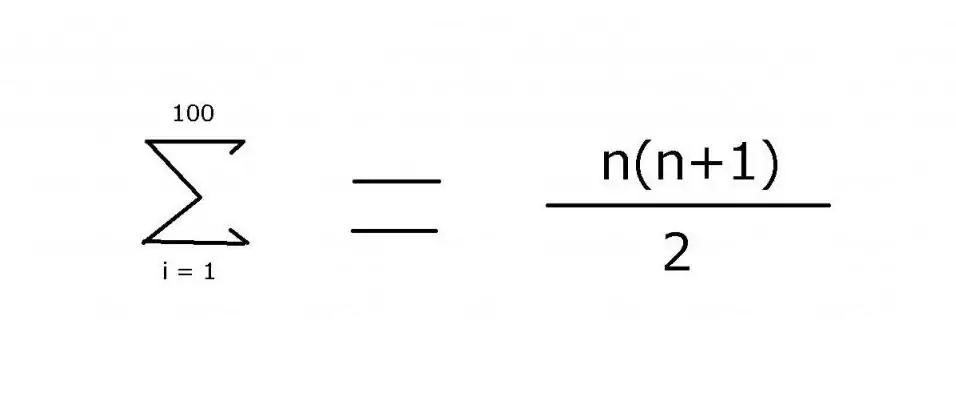
Thamani ya usemi huu ni 5050. Inaweza kupatikana kwa kutumia ujanibishaji wa hisabati, ambapo sehemu ya pili ya fomula ilitoka.
Kwa mfuatano tofauti, fomula itabadilika. Mchakato wa kurekodi umepunguzwa hadi kutafuta taswira ya awali ya mlolongo fulani usio na kikomo na kisha kuifafanua kwa fomula. Baada ya kufanya hivi, si vigumu kuelewa ni kiasi gani katika kesi fulani.
Inapohitajika kufafanua kuwa nambari zinaongezwa pamoja na ishara zake (pamoja na au kutoa), neno jumla ya aljebra hutumiwa. Kwa mfano, katika nadharia ya mzunguko wa umeme, sheria za mzunguko wa Kirchhoff huzingatia jumla ya aljebra ya mikondo katika mtandao wa kondakta zinazokutana katika hatua moja, ikitoa ishara tofauti kwa mikondo inayoingia na kutoka kwa nodi.






