Gesi bora, mlingano bora wa gesi wa hali, halijoto na shinikizo lake, kiasi… orodha ya vigezo na ufafanuzi unaotumika katika sehemu inayolingana ya fizikia inaweza kuendelea kwa muda mrefu sana. Leo tutazungumza tu juu ya mada hii.
Ni nini kinachozingatiwa katika fizikia ya molekuli?

Kitu kikuu kinachozingatiwa katika sehemu hii ni gesi bora. Equation bora ya gesi ya serikali ilipatikana kwa kuzingatia hali ya kawaida ya mazingira, na tutazungumzia kuhusu hili baadaye kidogo. Sasa hebu tuliendee "tatizo" hili kwa mbali.
Wacha tuseme tuna wingi wa gesi. Hali yake inaweza kuamua kwa kutumia vigezo vitatu vya asili ya thermodynamic. Hizi ni, bila shaka, shinikizo, kiasi na joto. Equation ya hali ya mfumo katika kesi hii itakuwa formula ya uhusiano kati ya vigezo vinavyolingana. Inaonekana hivi: F (p, V, T)=0.
Hapa, kwa mara ya kwanza, polepole tunakaribia kuibuka kwa kitu kama bora.gesi. Inaitwa gesi ambayo mwingiliano kati ya molekuli hauwezekani. Kwa ujumla, hii haipo katika asili. Walakini, gesi yoyote ambayo haipatikani sana iko karibu nayo. Nitrojeni, oksijeni na hewa, ambazo ziko chini ya hali ya kawaida, hutofautiana kidogo na bora. Kuandika equation ya serikali kwa gesi bora, tunaweza kutumia sheria ya umoja wa gesi. Tunapata: pV/T=const.
Dhana Husika 1: Sheria ya Avogadro
Anaweza kutuambia kwamba ikiwa tutachukua idadi sawa ya moles ya gesi yoyote ya nasibu kabisa na kuiweka katika hali sawa, ikiwa ni pamoja na joto na shinikizo, basi gesi zitachukua kiasi sawa. Hasa, jaribio lilifanyika chini ya hali ya kawaida. Hii ina maana kwamba halijoto ilikuwa 273.15 Kelvin, shinikizo lilikuwa angahewa moja (milimita 760 za zebaki, au 101325 Pascals). Kwa vigezo hivi, gesi ilichukua kiasi sawa na lita 22.4. Kwa hiyo, tunaweza kusema kwamba kwa mole moja ya gesi yoyote, uwiano wa vigezo vya nambari itakuwa thamani ya mara kwa mara. Ndiyo maana iliamuliwa kuteua takwimu hii na barua R na kuiita mara kwa mara ya gesi ya ulimwengu wote. Kwa hivyo, ni sawa na 8.31. Kizio ni J/molK.
Gesi bora. Mlinganyo bora wa hali ya gesi na upotoshaji wake
Hebu tujaribu kuandika upya fomula. Ili kufanya hivyo, tunaandika kwa fomu hii: pV=RT. Ifuatayo, tunafanya hatua rahisi, kuzidisha pande zote mbili za equation kwa idadi ya kiholela ya moles. Tunapata pVu=uRT. Hebu tuzingatie ukweli kwamba bidhaa ya kiasi cha molar nakiasi cha maada ni ujazo tu. Lakini baada ya yote, idadi ya moles itakuwa wakati huo huo sawa na mgawo wa wingi na molekuli ya molar. Hivi ndivyo mlinganyo wa Mendeleev-Clapeyron unavyoonekana. Inatoa wazo wazi la aina gani ya mfumo wa gesi bora. Mlinganyo wa hali ya gesi bora utachukua fomu: pV=mRT/M.
Tambua fomula ya shinikizo
Wacha tufanye upotoshaji zaidi kwa misemo iliyopatikana. Ili kufanya hivyo, upande wa kulia wa equation ya Mendeleev-Clapeyron huongezeka na kugawanywa na nambari ya Avogadro. Sasa tunaangalia kwa uangalifu bidhaa ya kiasi cha dutu na nambari ya Avogadro. Hii si chochote ila jumla ya idadi ya molekuli katika gesi. Lakini wakati huo huo, uwiano wa mara kwa mara wa gesi ya ulimwengu wote kwa nambari ya Avogadro itakuwa sawa na mara kwa mara ya Boltzmann. Kwa hiyo, kanuni za shinikizo zinaweza kuandikwa kama ifuatavyo: p=NkT/V au p=nkT. Hapa alama n ni mkusanyiko wa chembe.
Michakato bora ya gesi
Katika fizikia ya molekuli kuna kitu kama isoprocesses. Hizi ni taratibu za thermodynamic zinazofanyika katika mfumo katika moja ya vigezo vya mara kwa mara. Katika kesi hiyo, wingi wa dutu lazima pia kubaki mara kwa mara. Hebu tuziangalie kwa uwazi zaidi. Kwa hivyo, sheria za gesi bora.
Shinikizo hubaki bila kubadilika
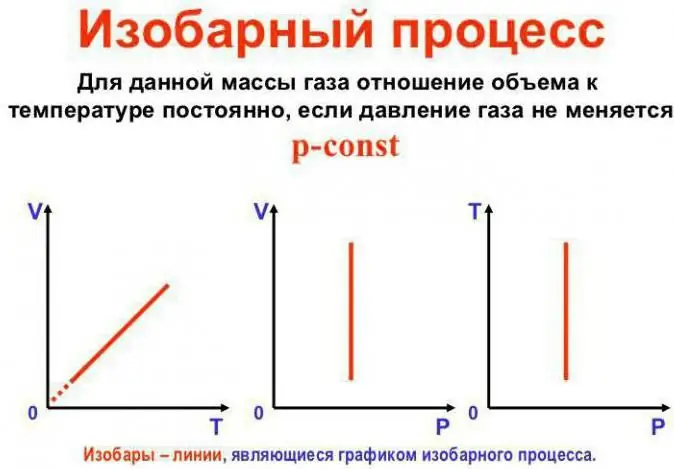
Hii ni sheria ya Gay-Lussac. Inaonekana kama hii: V/T=const. Inaweza kuandikwa upya kwa njia nyingine: V=Vo (1 + saa). Hapa a ni sawa na 1/273.15 K^-1 na inaitwa "mgawo wa upanuzi wa kiasi". Tunaweza kubadilisha halijoto katika Celsius nakiwango cha Kelvin. Katika kesi ya mwisho, tunapata fomula V=Voat.
Volume hubaki bila kubadilika

Hii ni sheria ya pili ya Gay-Lussac, ambayo inajulikana zaidi kama sheria ya Charles. Inaonekana kama hii: p/T=const. Kuna uundaji mwingine: p=po (1 + saa). Mabadiliko yanaweza kufanywa kwa mujibu wa mfano uliopita. Kama unavyoona, sheria bora za gesi wakati mwingine hufanana kabisa.
Joto hubaki sawa

Iwapo halijoto ya gesi bora itaendelea kudumu, basi tunaweza kupata sheria ya Boyle-Mariotte. Inaweza kuandikwa hivi: pV=const.
Dhana Husika 2: Shinikizo Kiasi
Tuseme tuna chombo chenye gesi. Itakuwa mchanganyiko. Mfumo huo ni katika hali ya usawa wa joto, na gesi wenyewe hazifanyiki kwa kila mmoja. Hapa N itaashiria jumla ya idadi ya molekuli. N1, N2 na kadhalika, kwa mtiririko huo, idadi ya molekuli katika kila sehemu ya mchanganyiko. Hebu tuchukue formula ya shinikizo p=nkT=NkT/V. Inaweza kufunguliwa kwa kesi maalum. Kwa mchanganyiko wa vipengele viwili, formula itachukua fomu: p=(N1 + N2) kT/V. Lakini basi inageuka kuwa shinikizo la jumla litafupishwa kutoka kwa shinikizo la sehemu ya kila mchanganyiko. Kwa hivyo, itaonekana kama p1 + p2 na kadhalika. Hizi zitakuwa shinikizo la kiasi.
Ni ya nini?
Mchanganyiko tuliopata unaonyesha kuwa shinikizo katika mfumo linatoka kwa kila kundi la molekuli. Kwa bahati mbaya, haitegemeiwengine. D alton alichukua fursa hii wakati wa kuunda sheria, ambayo baadaye ilipewa jina lake: katika mchanganyiko ambapo gesi haziingiliani kwa kemikali, shinikizo la jumla litakuwa sawa na jumla ya shinikizo la sehemu.






